Das Licht der Sterne wird mit einem Spektroskop zerlegt. Dabei werden Emissions- und Absorptionslinien sichtbar. Diese Linien werden mit den Werten verglichen, die man im Labor ermittelt hat, z.B. vom Wasserstoff oder Helium. Für Berechnungen kann man die Frequenz oder Wellenlänge der gemessenen Linien verwenden. Es werden jedoch die Wellenlängen bevorzugt. Um sich ein Bild davon zu machen, wie die Streckung einer Schwingung funktioniert, zeichnet man sich ein Anschauungsmodell.

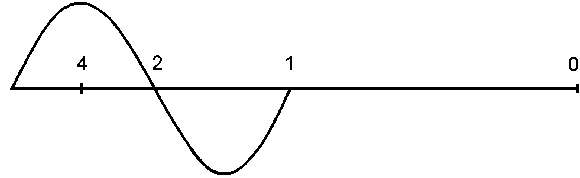
Abb. 1

Die Grundlinie der Abb. 1 hat die Strecke 2 π = 6,28. Zieht man nun die Sinuskurve bis zum rechten Ende der Grundlinie, so liegt sie deckungsgleich ohne Erhebung auf der Grundlinie. Damit hat man nachgewiesen, dass eine Schwingung durch Raumausdehnung an einem bestimmten Punkt den Wert Null erreicht.

Die Wellenlänge des Lichts wird während der Lichtlaufstrecke im Vakuumraum durch die Raumausdehnung gestreckt. Addiert man mehrere Raumausdehnungsgebiete, so erreicht die Raumausdehnung an einem bestimmten Abstand vom Beobachtungsstandort die Lichtgeschwindigkeit und damit die Informationsgrenze (Abb. 2).
Mit dieser Grenze hat man eine berechenbaren Größe innerhalb des Weltalls bestimmt.

Herleitung der Informationsgrenze:
c = Lichtgeschwindigkeit = 299 792,458 km s^-1
H_o = Expansions-Beschleunigung pro Raumausdehnungsgebiet (Hubble-Parameter)
r_i = Lichtlaufstrecke (Radius) vom Beobachtungsstandort bis zur Informationsgrenze
Präzisionsmessungen (April 2003) bestimmten den Hubble-Parameter mit   H_o = 71 km s^-1 Mpc^-1
Die standardisierte Entfernung (Megaparsec) wurde auf   Mpc = 3 261 631 Lichtjahre festgelegt.

Die Entfernung vom Beobachtungsstandort bis zur Informationsgrenze wird berechnet: r_i = c / H_o
r_i = 299 792,458 km s^-1 / 71 km s^-1 Mpc^-1 =
Aufgerundet sind das 13,8 Milliarden Lichtjahre und abgerundet sind das 13,7 Milliarden Lichtjahre.

Es gibt eine gesetzliche Beziehung von Wellenlänge und Frequenz zur Lichtgeschwindigkeit.
Dabei ist die Frequenz die Anzahl der Wellenlängen.
Das Ergebnis aus dem Produkt der Faktoren Wellenlänge mal Frequenz ergibt die Lichtgeschwindigkeit.
c = Lichtgeschwindigkeit
λ = Wellenlänge des Lichts
f = Frequenz des Lichts
c = λ * f

Herleitung des Expansionsfaktors:
Die beobachtete Wellenlänge (λ) der Lichtemission eines Sterns dividiert durch die im Labor gemessene Wellenlänge (λ_o)  ergibt den Streckungs-Faktor, bzw. Expansions-Faktor (z_e) für die Wellenlänge.
Doppelte Streckung ergibt eine Verdopplung der Wellenlänge.
z_e = λ / λ_o         Die z_e-Werte beginnen am Beobachtungsort mit 1.

Die herkömmliche Darstellung für die relative Rotverschiebung ist:
z = Δ λ / λ_o      Die z-Werte beginnen am Beobachtungsort bei Null.
Delta Lambda (Δ λ) ist die Differenz zwischen der beobachteten Wellenlänge und
der Labor-Wellenlänge (λ_o) Lambda Null.
Für präzise Berechnungen muss man aber die  z-Werte  in den Expansions-Faktor  (z_e)  umrechnen.
z_e = 1 + z

Die radiale Entfernung (r) eines Objekts wird wie folgt berechnet:
r_i = Radius vom Beobachtungsstandort bis zur Informationsgrenze
r = r_i - ( r_i / z_e )      oder nach Formelumstellung    r = r_i * (1 - 1 / z_e )
Man kann die Entfernung auch mit dem Wert der relativen Rotverschiebung (z) berechnen:
r = r_i - ( r_i / ( 1 + z ))      oder nach Formelumstellung    r = r_i * (1 - 1 / ( 1 + z ))

Berechnungsbeispiel:
Die Beobachtung einer fernen Galaxie ergab einen Wert von  z = 3.
Der Expansions-Faktor ist dann  z_e = 1 + z  =  1 + 3  =  4
Die Galaxie befindet sich damit in der Entfernung (r): Gesamtstrecke bis zur Informationsgrenze minus Rest-Strecke, in diesem Fall 1/4 der Gesamtstrecke bis zur Informationsgrenze.  r = r_i * ( 1 - 1 / 4 ) =  Mpc (Megaparsec)

Eine scheinbare Fluchtgeschwindigkeit, die größer ist als die Lichtgeschwindigkeit, kann nicht beobachtet werden. Aus diesem Grunde beziehen sich alle Berechnungen auf den Bereich der Lichtlaufstrecke vom Beobachtungsstandort bis zur Informationsgrenze. Die Entfernung wird durch den optischen Lichtreiseweg im Vakuumraum bestimmt.
Die scheinbare Fluchtgeschwindigkeit (v) eines Objekts wird wie folgt berechnet:    v = c - c / z_e
Nach Formelumstellung erhalte ich:    v = c * (1 - 1 / z_e )
v = c - c / (1 + z)   oder nach Formelumstellung   v = c * (1 - 1 / ( 1 + z ))

Die Expansionsbeschleunigung des Vakuumraumes ist als Hubble-Parameter definiert.
Entfernungs- und Geschwindigkeitsangaben werden durch diesen Parameter bestimmt.
Dieser Parameter hat eine statistische Schwankungsbreite aufgrund von unterschiedlichen Messergebnissen.

Im Jahre 1994 war die Schwankungsbreite:     H_o =   (40 km/sec) / Mpc   bis   (90 km/sec) / Mpc
Im Jahre 1997 war die Schwankungsbreite:     H_o =   (50 km/sec) / Mpc   bis   (80 km/sec) / Mpc
Im Jahre 2001 war die Schwankungsbreite:     H_o =   (60 km/sec) / Mpc   bis   (70 km/sec) / Mpc
Der statistische Mittelwert lag dabei immer bei   H_o = 65 km s^-1 Mpc^-1

Alle Werte innerhalb dieser Schwankungsbreiten wurden als korrekt angenommen.
Spätere Messungen mit dem Hubble-Space-Telescope legten den Wert auf   H_o = 73 km s^-1 Mpc^-1   fest.
Präzisionsmessungen (April 2003) bestimmten den Hubble-Parameter mit   H_o = 71 km s^-1 Mpc^-1
Die standardisierte Entfernung (Megaparsec) wurde auf   Mpc = 3 261 631 Lichtjahre festgelegt.
Dabei muss man bedenken, dass dieses Entfernungsmaß ein Maß für die optische Lichtreisezeit im Vakuum ist. Präzisionsmessungen könnten in Zukunft auch dieses standardisierte Entfernungsmaß neu festlegen.

Wir wollen nun aufgrund dieser Überlegungen die Entfernung einer Galaxie bestimmen. Vom Spektroskop wurde eine Emissionslinie vom Licht einer Galaxie gemessen.
Es ist die Grundspektrallinie des Wasserstoffs. Sie hat die Wellenlänge λ = 243,2 nm.
Die gleiche Emissionslinie wurde im Labor mit einer Wellenlänge λ_o = 121,6 nm bestimmt.
Die gemessene Streckung der Wellenlänge berechnet sich wie folgt: z_e = λ / λ_o
z_e = 243,2 nm / 121,6 nm = 2
Lichtgeschwindigkeit: c = 299 792,458 km s^-1

Die Entfernung vom Beobachtungsstandort bis zur Informationsgrenze wird berechnet: r_i = c / H_o
r_i = 299 792,458 km s^-1 / 71 km s^-1 Mpc^-1 =

Die radiale Fluchtgeschwindigkeit (v) des astronomischen Objekts bei einem z_e = 2 wird berechnet: v = c - (c / z_e )
v = 299 792,458 km/s - (299 792,458 km/s / 2) = 149 896,229 km/s
Die radiale Entfernung berechnet sich wie folgt: r = v / H_o oder   r = r_i - (r_i / z_e )   oder   r = r_i * (1 - 1 / z_e )
r = 149 896,229 km s^-1 / 71 km s^-1 Mpc^-1 =

Dieses Ergebnis ist korrekt. Das untersuchte Objekt entfernt sich mit 50% der Lichtgeschwindigkeit von unserem Beobachtungsstandort. Das ist genau die halbe Entfernung bis zur Informationsgrenze. Das Licht eines astronomischen Objekts bewegt sich durch das Vakuum auf den Beobachter zu. Während seiner Wanderung durch das Weltall dehnt sich das Vakuum aus. Mit der Ausdehnung des Vakuums wird die Wellenlänge des ausgestrahlten Lichts durch die Raumausdehnung gestreckt. Das Verhältnis zwischen der empfangenen Wellenlänge zur emittierten Wellenlänge ist mit der Raumausdehnung verknüpft. Mit der Berechnung der Lichtlaufzeit von der fernen Strahlungsquelle bis zum Standort des Beobachters wird die Entfernung des astronomischen Objekts bestimmt. Jede Information aus dem Weltall kommt aus der Vergangenheit. Will man den genauen heutigen Standort der fernen Lichtquelle bestimmen, kann man eine logische Wahrscheinlichkeits-Prognose abgeben, die man jedoch nicht mit Fakten beweisen kann. Das Wissen über die Vergangenheit erhalten wir nur aus dem Informationsgehalt des empfangenen Lichts. Die Behauptung, dass die fernen Galaxien und Quasare relativistische Geschwindigkeiten annehmen, ist somit ein Trugschluss. Die Behauptung, dass der Mittelwert des Hubble-Parameters eine Konstante ist, hat sich als Irrtum herausgestellt. Der Hubble-Parameter ist nie konstant gewesen. Die Linearität der Hubble-"Konstante" und ihre Konstanz bleibt wohl eine Wunschvorstellung der Astronomen.

Berechnungen von   z_e   mit der Frequenz der Absorptionslinie:
f   = Frequenz der gemessenen Absorptionslinie eines Objekts
f_o = Frequenz der im Labor gemessenen Absorptionslinie
z_e   = f_o / f
Die oben genannten Berechnungsmethoden entsprechen dem kosmischen Prinzip, dass keine Richtung im Kosmos einer anderen Richtung bevorzugt wird.

1. Verteilung der Spiralgalaxien im Weltraum.

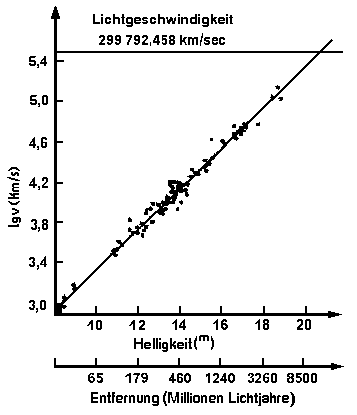
Abb. 2

Die Abb. 2 zeigt die Fluchtgeschwindigkeit von beobachteten Galaxien in Abhängigkeit von der Entfernung nach Sandage (1972). Als Senkrechte ist der Logarithmus der Fluchtgeschwindigkeit von den hellsten Galaxien dargestellt und auf der Zeitachse deren Abstand von der Erde. Das Weltall dehnt sich beschleunigt aus. In einer sehr großen Entfernung vom Beobachter erreicht die scheinbare Fluchtgeschwindigkeit der Galaxien die Lichtgeschwindigkeit. Von dort kann kein Licht den Beobachter auf der Erde erreichen. Die Informationsgrenze ist damit definiert (Schnittpunkt der beiden Graphen).
Der Logarithmus der Lichtgeschwindigkeit beträgt:   log   5.476820703

Daraus ergeben sich folgende Beweise:

1. Eine scheinbare Fluchtgeschwindigkeit, die größer ist als die Lichtgeschwindigkeit, kann nicht beobachtet werden. Aus diesem Grunde beziehen sich alle Beobachtungen und Berechnungen auf den Bereich der Lichtlaufstrecke vom Beobachtungsstandort bis zur Informationsgrenze.
2. Die Informationsgrenze definiert nicht das Alter oder das Ende des Weltalls.
3. Die kosmische Hintergrundstrahlung mit einer Temperatur von 2.725° Kelvin ist nur innerhalb des Bereichs der Lichtlaufstrecke vom Beobachtungsstandort bis zur Informationsgrenze zu beobachten.
   Ihre Abbildung entspricht der unregelmäßigen Verteilung der Galaxien und ihrer Haufenbildung.
   Die kosmische Hintergrundstrahlung wird sich verändern, aber sie wird nicht verschwinden.
4. Ein ausgestrahltes Photon kann sich nicht über das gesamte Weltall ausbreiten, sondern maximal nur bis zu seiner eigenen radialen Informationsgrenze.
5. Die Photonen, die ihre Strahlungsquelle verlassen haben, bewegen sich unabhängig von ihrer Lichtquelle durch den Vakuumraum.
6. Durch die Expansion des Vakuumraumes werden die Wellenlängen des Lichts während der Lichtlaufzeit gestreckt. Dies ergibt den Frequenzverlust des Lichtes. Je weiter eine Galaxie entfernt ist, umso schwächer rot leuchtet sie.
7. Die Gravitationskraft eines Sterns oder einer Galaxie reicht nicht unendlich weit ins Weltall hinaus, sondern maximal nur bis zu seiner eigenen radialen Informationsgrenze. Mit diesem Beweis wird eines der größten Irrtümer in der Kosmologie und der Physik beseitigt.
8. Die fernen Spiralgalaxien bewegen sich ebenso wie unsere Milchstraße nicht mit Lichtgeschwindigkeit in ihrem lokalen Vakuumraum. Mit diesem Beweis ist ein weiterer großer Irrtum der Kosmologie, dass die fernen Spiralgalaxien relativistische Geschwindigkeiten annehmen, beseitigt.

Bei der modernsten Meßmethode für die Bestimmung der fernen Galaxien wird nicht nur die scheinbare Helligkeit, sondern auch das Frequenzspektrum und die Anzahl der empfangenen Photonen pro Sekunde und ihre Energie gemessen.

Den Weltraum können wir nur von der Erde und von der erdnahen Umgebung betrachten. Als Beobachter hat man das Empfinden, dass man sich genau im Zentrum des gesamten Weltalls befindet. Das ist jedoch eine Täuschung. Das Weltall ist keine Materiekugel. Um sich ein Bild von der Verteilung der Spiralgalaxien im Weltall zu machen, zeichnet man sich ein Anschauungsmodell. Die Beschleunigungen pro Strecke werden so lange addiert, bis die Lichtgeschwindigkeit (c) erreicht ist.
Um keine Verwechslungen mit traditionellen Redshift-Werten   z = (λ / λ_o ) - 1   aufkommen zu lassen, die Werte für für den Expansionsfaktor ( z_e ) sind nach der Berechnungsmethode   z_e = λ / λ_o   angegeben.

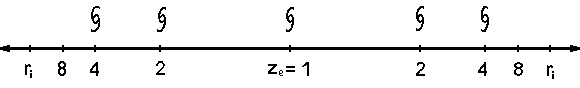
Abb. 3

Die absoluten Beobachtungsgrenzen sind an beiden Seiten der Strecke mit ( r_i ) angegeben. Die Pfeile in der Abb. 3 weisen darauf hin, dass das Weltall über die Informationsgrenze (r_i) hinaus sich weiter ausdehnt. Der Beobachter befindet sich auf der Erde bei der Position   z_e = 1. Dies ist nicht das kosmische Zentrum. Würde sich die Position des Beobachters auf der linken Seite der Abb.3 bei Ziffer 2 befinden, so ist dann für ihn die absolute Informationsgrenze der Ort bei der rechten Ziffer 2.

Die radiale Fluchtgeschwindigkeit ist: v = c - (c / z_e )  oder nach Formelumstellung   v = c * ( 1 - 1 / z_e )
Die Entfernung (r) berechnen man:
r = r_i * ( 1 - 1 / z_e )
r = r_i * ( 1 - 1 / ( 1 + z ))
Bei einem Expansionsfaktor von   z_e = 1   ist die scheinbare Fluchtgeschwindigkeit   v = c - (c / 1 )   gleich Null.

Beim Betrachten der Abb. 3  kann man sich die Frage stellen: "Wo befindet sich eigentlich das kosmische Zentrum?"
Das Licht der Galaxie von z_e = 2 auf der linken Seite der Grafik erreicht niemals die Galaxie bei z_e = 2 auf der rechten Seite der Grafik. Dort erreicht das Licht aufgrund der Streckung seine physikalische Grenze.
Für den Beobachter auf der Erde bei z_e = 1 sind jedoch beide Galaxien zu beobachten.
Fazit ist: Das kosmische Zentrum kann nicht bestimmt werden, weil es kein Zentrum im Weltall gibt.

Bis zu einer Entfernung von z_e = 2 sind mit Spiegelteleskopen noch Spiralgalaxien zu erkennen. Ihre scheinbare Fluchtgeschwindigkeit hat die halbe Lichtgeschwindigkeit erreicht. Zur Zeit werden die Instrumente zur Beobachtung des Weltraums immer weiter verbessert, so dass auch bei Entfernungen von   z_e  > 3   weitere Spiralgalaxien zu entdecken sind.
Bei   z_e = 4   sind die meisten Quasare zu erkennen. Der uns fernste Quasar liegt bei   z_e = 7.
Die scheinbare Fluchtgeschwindigkeit des fernen Quasars erreicht 85,7 % der Lichtgeschwindigkeit. Der uns nächste Quasar liegt bei einer Milliarde Lichtjahre. Quasare haben im Spektrum ihres Nachleuchtens eine hohe Rotverschiebung ihrer Spektrallinien. Eine weitere Eigenschaft der Quasare ist, dass sie höchstenergetisches Licht aussenden. Das Licht der fernen Spiralgalaxien kommt bei uns sehr schwach an. Aus diesem Grund sind sie schwieriger nachzuweisen. Es wird vermutet, dass Quasare aktive Übergangsstadien in der Entwicklungsgeschichte von Spiralgalaxien sind. Ein Beispiel [1] dafür ist die Galaxie M87. Diese Galaxie sendet einen "High-Energy-Jet" aus ihrem Zentrum heraus.

Je weiter die Galaxien vom Beobachter entfernt sind, umso weniger Licht kommt bei den Spiegelteleskopen an. Bei Entfernungen von   z_e   > 8   werden von den Spiegelteleskopen keine verwertbaren Lichtsignale im sichtbaren Bereich empfangen. Diese Lichtsignale liegen dann schon im Infrarotbereich, die nur von Infrarotkameras zu empfangen sind.

2. Kosmische Hintergrundstrahlung

Da die kosmische Hintergrundstrahlung von 2,725 K von der Erde aus zu beobachten ist, liegt auch sie mit ihrem Frequenzspektrum innerhalb der Lichtlaufstrecke von der Informationsgrenze bis zum Beobachter. Die Intensität der Hintergrundstrahlung muss mit zunehmender Wellenlänge ihres Frequenzspektrums abnehmen, weil durch die zunehmende Entfernung immer weniger Strahlung den Beobachter erreicht. Durch die Verteilung der Galaxien im Vakuumraum des Kosmos, ist die Hintergrundstrahlung aus allen Himmelsrichtungen nicht absolut gleich. Zur Begründung: Galaxien, die wir im Vordergrund sehen, verdecken andere Galaxien im Hintergrund. Messungen des Satteliten "Cobe" bestätigen geringe Abweichungen.

Octave ze-Value % Distance 0 1 0,00 1 2 50,00 2 4 75,00 3 8 87,50 4 16 93,75 5 32 96,88 6 64 98,44 7 128 99,22 8 256 99,61 9 512 99,80 10 1024 99,90

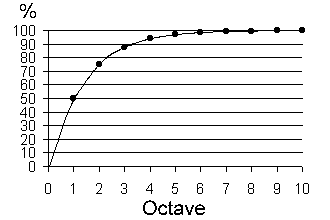
Abb. 4

Durch die Expansion des Vakuumraumes werden die Wellenlängen des Lichts während der Lichtlaufzeit gestreckt. Doppelte Streckung ergibt eine Verdopplung der Wellenlänge. Analog zur Musik verdoppelt sich die Frequenz von Oktave zu Oktave zu den höheren Tönen hin. Umgekehrt verdoppelt sich die Wellenlänge von Oktave zu Oktave zu den tieferen Tönen hin. Dies ist der Grund für die Einführung der Oktaven in das Maßsystem für große Entfernungen.

Die Werte für   z_e sind nach der Berechnungsmethode   z_e = λ / λ_o   angegeben. Durch die Expansion des Vakuumraumes werden die Wellenlängen des Lichts während der Lichtlaufzeit gestreckt. Von Oktave zu Oktave verdoppelt sich die Wellenlänge des empfangenen Lichts. Die in der Tabelle angegebenen Werte für "% Distance" kann man auch für die Bestimmung der scheinbaren Fluchtgeschwindigkeit verwenden, und zwar als % Angabe der Lichtgeschwindigkeit. Ein Beispiel: Objekte der 4. Oktave haben einen Wert von z_e = 16 und eine scheinbare Fluchtgeschwindigkeit von 93,75 % der Lichtgeschwindigkeit. Ihre Entfernung vom Beobachter beträgt 93,75 % der Strecke bis zur Informationsgrenze. Objekte ab der 4. Oktave können mit den leistungsstärksten Instrumenten nicht aufgelöst werden. Ab einer Entfernung von 99,9 % der Strecke vom Beobachter bis zur Informationsgrenze befindet sich die kosmische Hintergrundstrahlung.

Berechnungen:
Ermittelt nach folgender Methode:   z_e = λ / λ_o
Die Werte der relativen Rotverschiebung (z) müssen in den Expansions-Faktor ( z_e ) umgerechnet werden:
z_e = 1 + z
Die radiale Fluchtgeschwindigkeit wird berechnet:  v = c - (c / z_e )  oder  v = c * ( 1 - 1 / z_e )
Die radiale Entfernung (r) vom Beobachter wird berechnet:  r = r_i * ( 1 - 1 / z_e )
Der Wert für H_o wurde ständig geändert. Sein statistischer Durchschnittswert war   H_o = 65 km s^-1 Mpc^-1
Präzisionsmessungen (April 2003) bestimmten den Hubble-Parameter mit   H_o = 71 km s^-1 Mpc^-1
Die Werte für z_e und H_o können für Berechnungen verändert werden.

Lichtgeschwindigkeit:   c = 299 792,458 km s^-1
Mittelwert des Hubble-Parameters:   H_o = 71 km s^-1 Mpc^-1
Lichtjahre pro Megaparsec:   Mpc = 3261631 LJ
Radiale Entfernung bis zur Informationsgrenze:   r _i = c /H_o =
Lichtlaufzeit bis zur Informationsgrenze:   t _i = Milliarden Lichtjahre

Testen Sie das Programm:
Die Eingabefelder sind farbig hinterlegt.
Beim Quasar PC1247 + 3406 wurde die Grundspektrallinie des Wasserstoffs gemessen.
Der gemessene Wert: λ = 717,1 nm
Der Laborwert ist: λ_o = 121,6 nm
Berechnung nach folgender Methode:   z_e = λ / λ_o        z_e = 717,1 nm / 121,6 nm = 5,8972

3. Quellenangabe

[1] NASA/ESA Hubble Space Telescope

Alle Rechte vorbehalten. Copyright © by Albert Bünger, Artlenburg
Die amtliche Beurkundung meiner Theorie dient nur der Sicherung meiner Urheberschaft und soll in diesem Zusammenhang keine wissenschaftliche Diskussion und Verifikation ersetzen. Ich habe hiermit nun den Weg über das Internet gewählt, da mir eine Veröffentlichung über Fach-Zeitschriften abgelehnt wurde. Theorien, die nicht dem Mainstream entsprechen, haben in der Wissenschaft kaum eine Chance. Ich möchte jedoch daran erinnern, dass diese Theorie seit Jahren im Internet bekannt ist und weltweit gelesen und kopiert wird.
First publication of this Theory : February 24, 2002
First official authentication of this Theory: February 03, 2003

E-Mail :   a.buenger@ngc1365.de

Copies can be made for education and private usage only

17652   Visits   This Document was printed from Internet   www.ngc1365.de   at