The received light from Galaxy-Objects was investigated by a spectroscope. Thereby lines of emission and absorption become visible. These lines are compared with values getting from the lab, par example lines from hydrogen or helium. For calculation you can use the frequency or the wavelength of spectral lines. Astronomers prefer the wavelength. To get an experience, how the wavelength was stretched, you can draw a visual object.

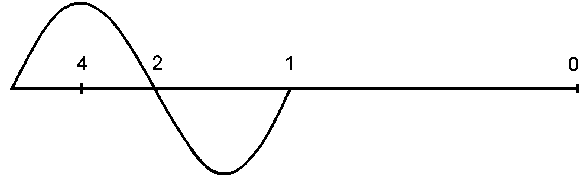
Ill. 1

The baseline of illustration 1 has the distance 2 π = 6.28. If you pull this wave to the right end of the baseline, you can see that the wave covers the baseline. The same matter happens, if the expanding vacuum-space of the cosmos has stretched the wavelength.

The wavelength of the light was stretched by the expanding vacuum-space of the cosmos. In this case the vacuum-space is a variable value. The expansion of the vacuum-space is reaching the light-speed in a certain distance from the observer. That is the point of the information-boundary. From that locality no light or other information can reach the observer. Look at Ill. 2. With this boundary you have determined a calculable size within the universe. You divide the light run distance from the local position of the observer up to the information boundary by 2. The remaining distances respectively divide by 2. You can make it like the example in the illustration 1 and 3. With that you have an excellent arithmetic base for the following calculation methods.

c = Light-Speed
λ = Wavelength
f = Frequency (Number of Wavelength)
c = λ * f

The expansion factor (z_e) is the result out of the relation between the measured wavelength (λ) of the light emission received from an astronomical object and the wavelength (λ_o) of a light emission measured in a laboratory.
z_e = λ / λ_o       Values begin with 1

Delta lambda (Δ λ) is the difference between the measured wavelength and the laboratory wavelength (λ_o) lambda zero.
z = Δ λ / λ_o     Values begin with zero

For precision calculation you have to convert the relative red schift (z) into the expansion factor  (z_e).
z_e = 1 + z

r_i = Distance from the locality of the observer to the Information-Boundary
H_o = Expansion-Acceleration per standardized expansion-distance (Hubble-Parameter)
c = Light-Speed
r_i = c / H_o

You cannot observe a flight speed, which is greater than the light speed. All calculation results are within the distance from the locality of the observer up to the locality of the Information Boundary.
λ_o = Wavelength of a light-emission measured in a lab
λ = Wavelength of a light emission measured from an astronomic object
v = flight speed calculated at the locality of the observer
v = c - c / z_e      or      v = c * (1 - 1 / z_e )
v = c - c / (1 + z)

The expansion-acceleration of the vacuum-space is defined by the Hubble-Parameter.
Distance- and speed-information are determined by this Parameter.
This parameter has an ordinary swing-width.

1994 the swing-width was by:     H_o =   (40 km/sec) / Mpc   til   (90 km/sec) / Mpc
1997 the swing-width was by:     H_o =   (50 km/sec) / Mpc   til   (80 km/sec) / Mpc
2001 the swing-width was by:     H_o =   (60 km/sec) / Mpc   til   (70 km/sec) / Mpc

Every values within these swing-width were assumed as correct. For this reason the definition "Hubble-Constant" is not correct. The new term "Mean-Value of the Hubble-Parameter" is correct, because his value contain the definition swing-width of variations.
Later measurements with the Hubble-Space-Telescope defined the value   H_o = 71 km s^-1 Mpc^-1
The standardized distance value (Mega parsec) was defined with   Mpc = 3 261 631 Light-years.
You have to remind that this distance-measure its a value of the optical light-travel-time in the vacuum of the cosmos. Precision-measurements in future can define this standardized distance-measure once more.

This is the foundation to calculate the distance of a Galaxy.
The spectroscope has measured an emission line from the light of a galaxy.
It is the main-wavelength of hydrogen (Lyman α ). The wavelength is λ = 243.2 nm.
The same spectral-line was measured in a lab with a wavelength of λ_o = 121.6 nm.
The measured stretching of the wavelength is calculated as follows: z_e = λ / λ_o
z_e = 243.2 nm / 121.6 nm = 2
Speed of Light: c = 299 792.458 km s^-1
Mean-value of the Hubble-Parameter: H_o = 71 km s^-1 Mpc^-1

The radial Information-Boundary was calculated: r_i = c / H_o
r_i = 299 792.458 km s^-1 / 71 km s^-1 Mpc^-1 =
The radial Flight-Speed was calculated: v = c - (c / z_e )
v = 299 792.458 km s^-1 - (299 792.458 km s^-1 / 2) = 149 896.229 km s^-1
The radial distance was calculated as follows: r = v / H_o
r = 149 896.229 km s^-1 / 71 km s^-1 Mpc^-1 =

This result is correct. The radial distance is exactly half the distance to the Information-Boundary and the observed object is fleeting away with 50% of the speed of light. The light-emission needs a certain time to reach the observer. During this time the wavelength was expanded by the expansion of the vacuum-space of the cosmos. This dependence is valid for every wavelength. Therefore you can use this calculation-method for all wavelength and frequencies.

Calculation of z_e with the frequency of the absorption-line:
f   = Frequency of the measured absorption-line of an object
f_o = Frequency of the measured absorption-line of the Lab
z_e   = f_o / f

1. Distribution of Spiral-Galaxies in the cosmos.

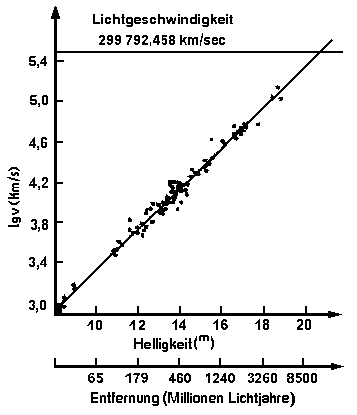
Ill. 2

The illustration 2 shows the flight speed and the distance of the brightest galaxies from the point of observation. Firstly find out by Sandage (1972). The vertical line displays the logarithm of the flight speed of the brightest Galaxies and the horizontal line displays the distance from the observer. The cosmos expands with acceleration. In a far distance from the observer the flight speed of the galaxies reached the light speed. The information boundary is determined by the point of intersection of both lines. The logarithm of the light speed is:   log   5.476820703

The following proofs arise from this:

1. A flight speed which is larger than the light speed cannot be observed. For this reason all observations and calculations refer to the area of the light run distance of the observation location up to the information boundary.
2. The cosmic background radiation has to be watched by the observation location only within the area of the light run distance up to the information boundary.
3. The information boundary doesn't define the age or the end of the universe.
4. A radiated photon cannot spread across the complete universe, but maximum only up to that one of his own radial information boundary.
5. The gravitation strength of a star or a galaxy only reaches up to his own radial information boundary. With this proof one of the greatest mistakes is removed in the cosmology and the physics.
6. By the expansion of the vacuum room the wavelengths of the light are stretched during the light running time. This yields the frequency loss of the light.
7. The distant spiral Galaxies don't move just like our Milky Way with light speed in their local vacuum room. With this proof another mistake of the cosmology is removed with that, that the distant spiral Galaxies assume relativistic speeds.

The most modern method to determine the far galaxies is the use of detectors which can count the quantity of the photons and measure their energy.

You can observe the vacuum room of the cosmos only from our location of our planet or the nearby region in the orbit. It seems to be to the observer, that he is in the center of the cosmos. That is an optical delusion. To get a vision from the distribution of the Spiral-Galaxies in the vacuum room of the universe, you can draw a visual model. To get no confusion with traditional values   z = (λ / λ_o) - 1, the values for the expansion factor   z_e   are calculated as follows   z_e = λ / λ_o

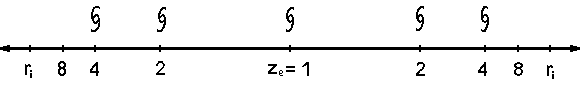
Ill. 3

You can recognize the absolute Information-Boundaries (r_i) at both ends of the line. The arrows give you the hint, that there is no end of the expansion of the cosmic vacuum-space. The observer lives on the planet of the Spiral-Galaxy at the position of  z_e = 1. The radial flight speed is: v = c - (c / z_e )   or   v = c * ( 1 - 1 / z_e )

If you use the expansion-factor   z_e = 1   than you will get a result of the flight speed of   v = c - (c / 1 ) = 0

Up to z_e = 2 the Mirror-Telescopes can recognize Spiral-Galaxies. Their flight speed have reached half of the light speed. At distances of z_e > 3 there are further Spiral-Galaxies to detect, because the quality of the mirrors and light detection will be improved in future. By z_e = 4 you can detect most of these Quasars. The most distant Quasar was found by z_e = 7. His flight-speed has reached 85.7% of the light-speed. The most next Quasar you can find by 1000 millions light-years. Quasars have a high red shift, visible at the Spectral-Lines of their afterglow. A further property of the Quasars is to transmit high energy light. There are assumptions, that Quasars are the active transitional phase of the development-history of Spiral-Galaxies. An example [1] for that is the Galaxy M87. This Galaxy has a high-energy-jet, that arise with a high speed up from the center of the Galaxy.

If the Galaxies are far enough, no light can be obtained by the mirror-telescopes. At distances of z_e > 8 mirror-telescopes cannot obtain any usable light-information in the visible range. Then these light signals already lie in the infrared area which are to be received only by infrared cameras.

2. Cosmic Background-Radiation

Astronomers have observed the 2.725 K background-radiation with the COBE-Satellite. This background-radiation is within the distance from local observer to the Information-Boundary too. The intensity of the background-radiation was reduced on dependence of the larger growing wavelength of their frequency-spectrum. Galaxies in foreground cover galaxies in the background. For that reason the background-radiation from all directions in the cosmos is not absolutely even. Measurements of the COBE-Satellite confirm this facts.

Octave ze -Value % Distance 0 1 0,00 1 2 50,00 2 4 75,00 3 8 87,50 4 16 93,75 5 32 96,88 6 64 98,44 7 128 99,22 8 256 99,61 9 512 99,80 10 1024 99,90

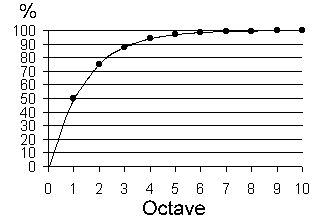Ill. 4

Analogously to the music the frequency doubles herself from octave to octave to the higher notes. The other way the wavelength doubles herself from octave to octave to the lower notes. This is the reason for the introduction of the octaves to the measurement system for large distances.

The values for   z_e   are calculated as follows   z_e = λ / λ_o. From one octave to the next octave, the value of the wavelength was multiplied with 2. The values displayed in the table for "% Distance" can be used for the determination of the apparent flight speed as % value of the light-speed. Par example, objects of the 4th octave have a value of z_e = 16 and a apparent flight speed of   93.75 % of the light speed. Their remoteness is   93.75 % of the distance from the local observer to the Information-Boundary. The Cosmic Microwave Background (CMB) has a remoteness of 99.9 % of the distance from the local observer to the Information-Boundary.

Calculations:
Created with following method:   z_e = λ / λ_o
The radial Flight-Speed was calculated: v = c - (c / z_e )   or   v = c * ( 1 - 1 / z_e )
You can convert traditional z-values to the expansion-factor ( z_e ) by the method:   z_e = 1 + z
The input for z-values are created with following method:   z = (λ / λ_o ) - 1   or   z = Δ λ / λ_o
In the history the value for the Hubble-Parameter ( H_o ) was changed very often. It was never constant.
If you like to calculate with other values, than you can change the values z_e and H_o

Speed of the light:   c = 299 792.458 km s^-1
Mean-Value of the Hubble-Parameter:  H_o = 71 km s^-1 Mpc^-1
Light years per Megaparsec:   Mpc = 3261631 Light-Years
Information-Boundary:   r _i = c / H_o =
Information-Boundary:   t _i = billion Light-Years
Latest standardized value:   H_o = 71 km s^-1 Mpc^-1

You can test this program:
Enter fields are background colored.
The basic-spectral-line of the hydrogen of the Quasar PC1247 + 3406 was measured.
The measured value was: λ = 717.1 nm
The measured value in the labor was: λ_o = 121.6 nm
Calculation with following method:   z_e = λ / λ_o        z_e = 717.1 nm / 121.6 nm = 5.8972

3. Source of Literary and Photo

[1] NASA/ESA Hubble Space Telescope

All rights preserved. Copyright © by Albert Bünger, Artlenburg
The official certification of my theory serves only the safeguarding of my authorship and in connection with this shall not replace any scientific discussion and verification. I have chosen the way hereby over the internet now, because an announcement over magazines was declined. Theories which don't correspond to the Mainstream have hardly a chance in the science. I would like to remind, however, that this theory is known in the internet since several years and is read and copied worldwide.
First publication of this Theory : February 24, 2002
First official authentication of this Theory: February 03, 2003

E-Mail :   a.buenger@ngc1365.de

Copies can be made for education and private usage only

Visits   This Document was printed from Internet www.ngc1365.de at